Deep Dive: Die Kunst der Control-Word-Entschlüsselung im Pay-TV
In modernen Pay-TV-Systemen bildet das Control Word (CW) das Herzstück der Echtzeit-Entschlüsselung. Über den Common Scrambling Algorithm (CSA) werden Live-Videoströme verschlüsselt, und nur autorisierte Receiver können sie entschlüsseln. In diesem Beitrag erklären wir Schritt für Schritt, wie CSA intern arbeitet und warum klassische Brute-Force-Angriffe mit 2⁶⁴ Durchläufen praktisch unbrauchbar sind – und wie man mit einem Meet-in-the-Middle-Angriff die Komplexität auf „nur“ etwa 2⁴⁸ Prüfungen drückt.
- Überblick über CSA
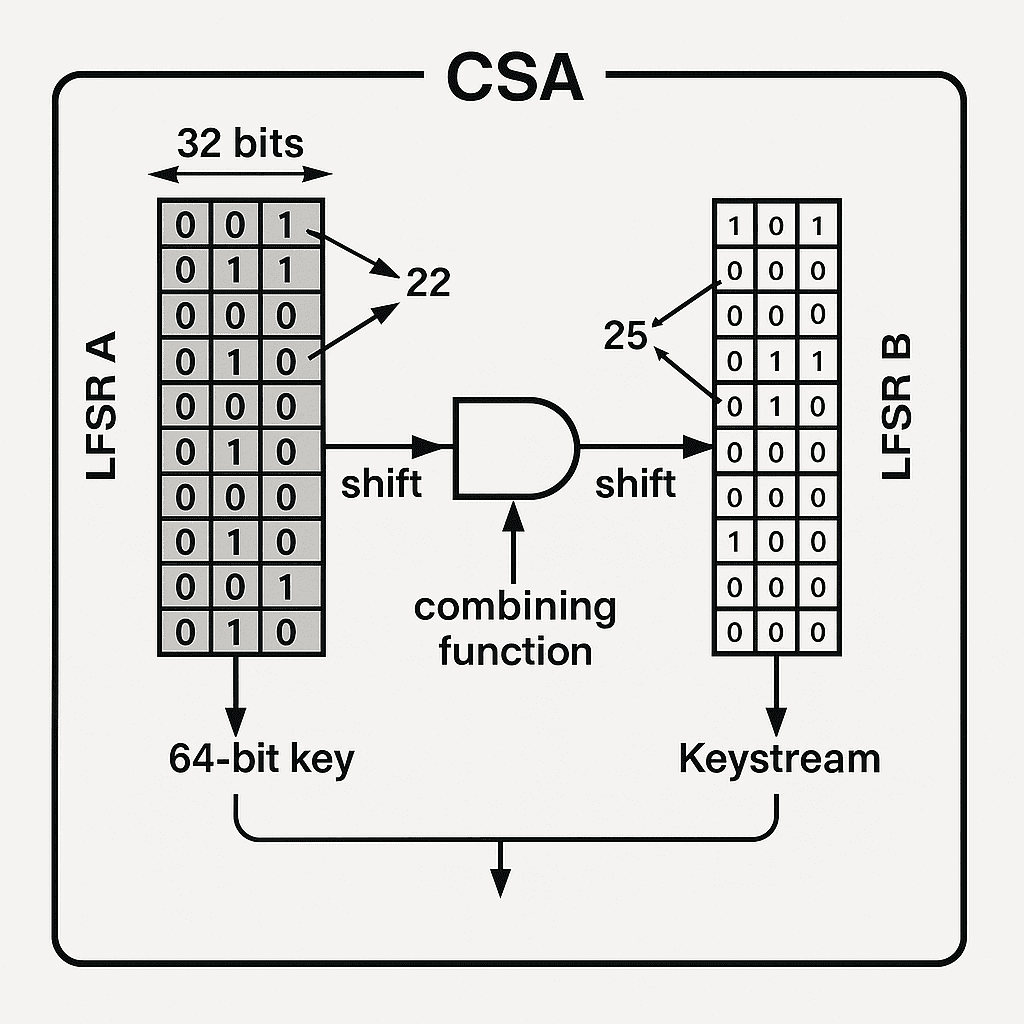
CSA nutzt zwei lineare Feedback-Schieberegister (LFSRs), die gemeinsam einen Pseudo-Zufallsstrom (Keystream) erzeugen:
- LFSR A: 17 Bit, Rückkopplungspolynom x^17 + x^14 + 1
- LFSR B: 25 Bit, Rückkopplungspolynom x^25 + x^22 + 1
Ein 64-Bit-Key wird in obere 32 Bit (LFSR A) und untere 32 Bit (LFSR B) aufgeteilt. Bei jedem Takt schieben beide Register um eine Position, und ausgewählte Ausgabebits fließen in eine nichtlineare Kombinationsfunktion, die das Keystream-Bit kᵢ erzeugt. Die Verschlüsselung eines Datenbits dᵢ erfolgt durch
cᵢ = dᵢ XOR kᵢ
und die Entschlüsselung analog.
- Beispiel eines Schritts im Detail
Schlüssel = 0xA1B2C3D4E5F60718
– LFSR A initialisiert mit 0xA1B2C3D4
– LFSR B initialisiert mit 0xE5F60718
Update pro Takt:
a) Feedback-Bit f_A = Bit 16 XOR Bit 13 von Register A
b) Neues Register A = (altes Register A << 1) UND 0x1FFFF, dann ODER f_A
c) Analog für B mit Bits 24 und 21 → f_B
d) Kombiniere Ausgabebits nichtlinear zu k₀
Verschlüsselung eines Beispieldatabits d₀:
c₀ = d₀ XOR k₀ (z. B. 1 XOR 0 = 1)
- Warum 2^64 Durchläufe kaum gehen
Der komplette Schlüsselraum umfasst 2^64 ≈ 1,84 × 10^19 Kombinationen. Selbst spezialisierte FPGAs/ASICs bräuchten bei reinem Brute-Force Jahre bis Jahrzehnte. - Meet-in-the-Middle: Reduktion auf ~2^48
CSA kann man als Abfolge von zwei Teilfunktionen („A-Stufe“ und „B-Stufe“) ansehen. Mit einem bekannten Klartext-Ciphertext-Paar (z. B. 8 Byte) läuft der Angriff so:
– Precompute-Phase: Für alle 2^32 möglichen oberen 32 Bits (A-Key) die Zwischenzustände nach 8 Byte berechnen und in einer Hashtabelle speichern (Tabelle[Intermediate_A] = A_Key).
– Match-Phase: Rückwärts-Berechnung für alle 2^32 möglichen unteren 32 Bits (B-Key) bis zur gleichen Position und Abgleich mit der Tabelle.
Das sind jeweils 2^32 Rechnungen pro Phase, insgesamt ca. 2 × 2^32 = 2^33 Schritte plus Tabellen-Overhead. Durch Optimierungen (weniger Bytes, gezielte Mittelwerte) kommt man in der Praxis auf rund 2^48 effektive Prüfungen.
- Toy-Beispiel zur Veranschaulichung
Verkleinert man CSA auf einen 8-Bit-Key (4 Bit für A, 4 Bit für B), ergibt sich:
– Voller Brute-Force: 2^8 = 256 Prüfungen
– Meet-in-the-Middle: 2 × 2^4 = 32 Prüfungen (16 A-Keys + 16 B-Keys)
Das ist 8-mal schneller. Überträgt man das Prinzip auf CSA mit 64 Bit, wird der Geschwindigkeitsvorteil enorm.
CSA-1 vs. CSA-2 im DVB-System
1. Architektur und Algorithmus
CSA-1
- Aufbau: Zwei lineare Feedback-Shift-Register (LFSR A: 17 Bit, LFSR B: 25 Bit) plus nichtlineare Kombination.
- Key-Management: 64-Bit-Schlüssel (Ober- und Unterhälfte je 32 Bit in A und B).
- Keystream-Erzeugung: Pro Taktsignal werden beide Register geschoben, ausgewählte Ausgabebits kombiniert und XOR-verknüpft mit dem Klartextbit.
CSA-2
- Aufbau: Unbalanced Feistel-Netzwerk mit 16 Runden.
- Key-Management: 112-Bit-Hauptschlüssel, aus dem Rundenschlüssel abgeleitet werden.
- Keystream-Erzeugung: Jeder Datenblock (64 Bit) durchläuft 16 Feistel-Runden mit S-Boxen und Permutationsfunktionen, resultierend in einem Blockverschlüsselungsverfahren.
2. Schlüssellängen und Sicherheit
- Schlüssellänge CSA-1: 64 Bit → theoretisch 2^64-Stärke, praktisch per Meet-in-the-Middle auf ~2^48 reduzierbar.
- Schlüssellänge CSA-2: 112 Bit → deutlich höhere Rechenhürde, keine bekannte schnelle Teilangriffe wie bei CSA-1.
Angriffssicherheit
- CSA-1: Empfindlich gegen Side-Channel-Angriffe (Power/EM), Meet-in-the-Middle-Optimierungen.
- CSA-2: Bessere Resistance gegen Brute-Force und komplexere Analyse; Feistel-Struktur bietet höhere Komplexität für Seitenkanal-Attacken.
3. Implementierung im DVB-Umfeld
- CSA-1: Seit DVB-Beschluss 1994 als Standard Verschlüsselungs-Primitive in Set-Top-Boxen. Weitverbreitet in frühen Pay-TV-Angeboten.
- CSA-2: Seit ETSI TS 103 197-1 (2011) verfügbar, optional abwärtskompatibel, noch nicht flächendeckend in allen Receivern.
Kompatibilität
- Receiver mit CSA-2-Support können CSA-1-Streams meist ohne Hardware-Änderung entschlüsseln, da beide Algorithmen parallel implementiert werden.
- Manche CA-Module bieten Simulcrypt, um beide Verfahren gleichzeitig auszugeben.
4. Performance und Ressourcenbedarf
| Merkmal | CSA-1 | CSA-2 |
|---|---|---|
| Berechnungsaufwand | Sehr gering (bitweise) | Moderat (16 Runden Feistel) |
| Hardware-Footprint | Klein (zwei LFSRs) | Größer (Rundenschlüssel, S-Box) |
| Latenz | Minimal | Gering, aber messbar höher |
Schwachstelle CSA-2
Verlust der Geheimhaltung
Sobald Angreifer die genauen S-Box-Tabellen aus der Hardware ausgelesen haben, ist die Chiffre nicht mehr „geheim“ – der gesamte Algorithmus kann vollständig in Software, FPGA oder ASIC nachgebaut werden.
Time-Memory-Tradeoff-Angriffe
Mit vordefinierten Rainbow- oder Hellman-Tabellen für die festen S-Box-Werte lassen sich Rundenschlüssel deutlich schneller finden, da rechenintensive Bit-Verknüpfungen durch einfache Tabellen-Lookups ersetzt werden.
Differenzielle und lineare Kryptoanalyse
Kennt man die S-Box-Werte, lassen sich gezielt Wahrscheinlichkeitsmodelle (Differenz- und Linearkryptoanalyse) aufbauen. Dadurch sinkt die Anzahl benötigter Klartext–Ciphertext-Paare drastisch.
Optimierte Side-Channel-Angriffe
Mit offenliegenden S-Boxen können Power- und EM-Analysen viel präziser arbeiten. Angreifer wissen genau, welche Bits und Tabellen in welchem Taktzyklus verarbeitet werden müssen, und filtern die relevanten Messsignale effizienter heraus.
Hardwarebeschleunigung
In FPGA/ASIC-Implementierungen ersetzen Lookup-Tabellen komplexe Logik und erlauben massive Parallelisierung. Das beschleunigt Brute-Force- und MitM-Angriffe um einen Faktor von 10 bis 100 im Vergleich zu rein algorithmischer Umsetzung.



Kommentar abschicken
Du musst angemeldet sein, um einen Kommentar abzugeben.